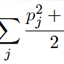NORMAL FORM AND ENERGY CONSERVATION OF HIGH FREQUENCY SUBSYSTEMS WITHOUT NONRESONANCE CONDITIONS

Abstract

We consider a system in which some high frequency harmonic oscillators are coupled with a slow system. We prove that up to very long times the energy of the high frequency system changes only by a small amount. The result we obtain is completely independent of the resonance relations among the frequencies of the fast system. More in detail, denote by ϵ⁻¹ the smallest high frequency. In the first part of the paper we apply the main result of [1] to prove almost conservation of the energy of the high frequency system over times exponentially long with ϵ^−1/n (n being the number of fast oscillators). In the second part of the paper we give a new self-contained proof of a similar result which however is valid only over times of order ϵ^−N with an arbitrary N. Such a second result is very similar to the main result of the paper [4], which actually was the paper which stimulated our work.