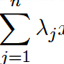Articoli
Volume 146 • (2012) Rendiconti - Classe di Scienze Matematiche e Naturali
https://doi.org/10.4081/scie.2012.186
ON A THEOREM OF LYAPOUNOV
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Ricevuto: 9 settembre 2015
Pubblicato: 30 dicembre 2012
Pubblicato: 30 dicembre 2012
826
Visite
838
Downloads
It is shown that a Hamiltonian system in the neighbourhood of an equilibrium may be given a special normal form in case the eigenvalues of the linearized system satisfy non–resonance conditions of Melnikov's type. The normal form possesses a two dimensional (local) invariant manifold on which the solutions are known. If the eigenvalue is pure imaginary then these solutions are the natural continuation of a normal mode of the linear system. The latter result was first proved by Lyapounov. The present paper completes Lyapounov's result in that the convergence of the transformation of the Hamiltonian to a normal form is proven and the condition that the eigenvalues be pure imaginary is removed.
Downloads
La data di download non è ancora disponibile.
Come citare
ON A THEOREM OF LYAPOUNOV. (2012). Istituto Lombardo - Accademia di Scienze e Lettere - Rendiconti di Scienze, 146. https://doi.org/10.4081/scie.2012.186